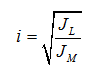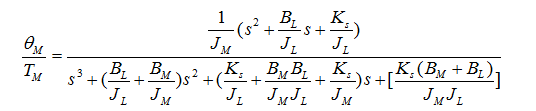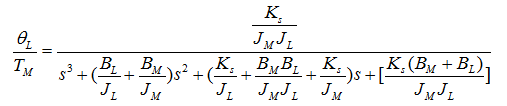【摘要】 慣量匹配是伺服系統(tǒng)設(shè)計(jì)中必須考慮的因素之一。本文主要分析了慣量匹配對伺服系統(tǒng)穩(wěn)定性及加速性能的影響并簡略提出了慣量匹配的實(shí)用性原則。

【關(guān)鍵字】慣量匹配、伺服系統(tǒng)、伺服控制策略

The Generalized Principle of Inertia Matching for Servo System

[Abstract]  Inertia Matching is one of the essential factors in servo system design. This paper briefly discusses the effects of inertia matching in stability and acceleration performance of servo system, and gives some practical advices of inertia matching for servo system. A strategy for servo control in presence of inertia mismatching is then introduced.

[Keywords]  Inertia Matching; Servo System; Strategy for Servo Control

0.        引言

在伺服控制系統(tǒng)設(shè)計(jì)或是伺服電機(jī)的選型過程中，常常需要考慮慣量問題，慣量是影響伺服系統(tǒng)響應(yīng)速度和穩(wěn)定性的重要因素?？偟膩碚f，是希望系統(tǒng)的總體慣量越小越好，因?yàn)楦〉南到y(tǒng)慣量意味著更大的加速能力和更快的瞬態(tài)響應(yīng)速度。在負(fù)載慣量一定的條件下，我們通常通過減小電機(jī)的轉(zhuǎn)子慣量來達(dá)到降低系統(tǒng)總體慣量的目的，但這樣的做法則不可避免的遇到慣量匹配的問題。

慣量匹配原則是指折算到電機(jī)軸的負(fù)載慣量與電機(jī)的轉(zhuǎn)子慣量之比不能過大，必須小于一個(gè)推薦值，當(dāng)慣量比過大時(shí)，系統(tǒng)一般會(huì)出現(xiàn)振蕩甚至失控。這樣一個(gè)原則被廣泛接受和使用，但是很少有人去深究其內(nèi)在的理論依據(jù)，伺服系統(tǒng)的設(shè)計(jì)者通常也并不十分清楚負(fù)載電機(jī)慣量比與系統(tǒng)穩(wěn)定性的深層關(guān)系，因此慣量匹配原則始終作為一個(gè)經(jīng)驗(yàn)法則存在著。

本文建立了一個(gè)簡單的物理模型，用于分析慣量匹配對系統(tǒng)控制的影響，并基于此分析得到關(guān)于慣量匹配的實(shí)用性建議，為更好的理解負(fù)載電機(jī)慣量比與系統(tǒng)穩(wěn)定性、響應(yīng)性能等之間的關(guān)系，更合理的利用慣量匹配原則提供參考。

1.        伺服系統(tǒng)建模

1.1               傳統(tǒng)模型

在傳統(tǒng)的伺服系統(tǒng)設(shè)計(jì)中，一般認(rèn)為負(fù)載和電機(jī)之間的傳動(dòng)裝置剛性是無窮大的，其模型示意圖如圖1：

圖1  簡單的電機(jī)——負(fù)載傳動(dòng)模型

設(shè)定電機(jī)的轉(zhuǎn)動(dòng)慣量為J_M；負(fù)載慣量為J_L；傳動(dòng)比為i；傳動(dòng)效率為η；傳動(dòng)裝置慣量為J_C；電機(jī)軸轉(zhuǎn)速為ω_M；電機(jī)軸輸出轉(zhuǎn)矩為T_M，系統(tǒng)滿足以下基本方程：

負(fù)載轉(zhuǎn)速ω_L：

負(fù)載轉(zhuǎn)矩T_L：

折算到電機(jī)軸的負(fù)載慣量J_LM：

從以上表達(dá)式可以看出，如果使用減速比為i的減速器連接負(fù)載和電機(jī)，電機(jī)輸出的轉(zhuǎn)速將會(huì)下降為原來的1/ i；而折算到電機(jī)軸上的慣量會(huì)下降為原來的1/ i²，對于大慣量負(fù)載而言，這是降低負(fù)載電機(jī)慣量比的有效方法，但是系統(tǒng)的加速轉(zhuǎn)矩也將會(huì)提高到原來的i倍。

如果系統(tǒng)滿足慣量匹配，一般認(rèn)為此時(shí)系統(tǒng)可以達(dá)到最大的能量傳遞效率，而負(fù)載也將獲得最大的加速性能。為了確定負(fù)載電機(jī)慣量比與系統(tǒng)加速性能之間的關(guān)系，對圖1中的系統(tǒng)作如下假定：

（1）       直接耦合到電機(jī)軸上的齒輪或皮帶輪的慣量作為電機(jī)轉(zhuǎn)子慣量的一部分；

（2）       直接耦合到負(fù)載軸上的齒輪或皮帶輪的慣量作為負(fù)載慣量的一部分；

（3）       忽略傳動(dòng)裝置的效率、摩擦和自身慣量等因素；

系統(tǒng)滿足方程：      （1）

電機(jī)的加速度為：（2）

其中為負(fù)載的加速度。

由（1）、（2）兩式可以推出，負(fù)載的加速度為：        （3）

電機(jī)的輸出轉(zhuǎn)矩T_M一定，要知道最大負(fù)載加速度時(shí)的慣量比，即需要知道確定最大負(fù)載加速度時(shí)對應(yīng)的傳動(dòng)比i的值，式（3）對i求導(dǎo)，得：    （4）

令式（4）等于0；得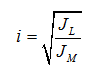：     （5）

由式（5）不難算出，當(dāng)負(fù)載獲得最大加速度時(shí)，折算到電機(jī)軸的負(fù)載慣量J_LM與電機(jī)轉(zhuǎn)矩J_M之比為1:1。從以上分析可知，在理想狀態(tài)下，調(diào)整負(fù)載電機(jī)慣量比為1:1有助于系統(tǒng)的加速性能。但在實(shí)際應(yīng)用過程中，由于傳動(dòng)裝置的效率，空程間隙等機(jī)械特性，傳動(dòng)裝置自身的慣性，負(fù)載的反沖作用，系統(tǒng)的傳動(dòng)剛性等諸多因素的影響，設(shè)置負(fù)載慣量比為1:1并不具有很高的效率，而且增加減速比的方式也會(huì)提高整個(gè)系統(tǒng)所需要的加速轉(zhuǎn)矩。在如上諸多因素中，系統(tǒng)的傳動(dòng)剛性是最需要考慮的問題，因?yàn)樵谙到y(tǒng)傳動(dòng)剛性較差的前提下，如果負(fù)載電機(jī)的慣量比過大將會(huì)導(dǎo)致系統(tǒng)振蕩，出于系統(tǒng)穩(wěn)定性的考慮，需要修改電機(jī)到負(fù)載的傳動(dòng)模型。

1.2               改進(jìn)模型

使用一根彈性軸作為連接負(fù)載和電機(jī)的傳動(dòng)裝置，忽略傳動(dòng)裝置的內(nèi)部細(xì)節(jié)，忽略彈性軸直徑等次要因素，僅僅將注意力放在傳動(dòng)剛性上，基于以上假設(shè)建立負(fù)載和電機(jī)之間的傳動(dòng)模型，其示意圖如圖2：

圖2  電機(jī)——負(fù)載彈性傳動(dòng)模型

圖中：T_M為電機(jī)的輸出轉(zhuǎn)矩；T_L為負(fù)載轉(zhuǎn)矩；B_M和B_L分別為電機(jī)和負(fù)載的粘性摩擦系數(shù)；K_S為彈性軸的抗扭剛度；ω_M和ω_L分別是電機(jī)和負(fù)載的轉(zhuǎn)速，θ_M和θ_L分別表示電機(jī)和負(fù)載角位移，θ_S為彈性軸的扭轉(zhuǎn)度。

J_M和J_L分別為電機(jī)和負(fù)載的轉(zhuǎn)動(dòng)慣量，系統(tǒng)滿足運(yùn)動(dòng)方程：

                （6）

                   （7）

                           （8）

使用式（6）、（7）、（8）可以得到電機(jī)和負(fù)載速度響應(yīng)，通過拉氏轉(zhuǎn)換求得其傳遞函數(shù)，分別表示為：

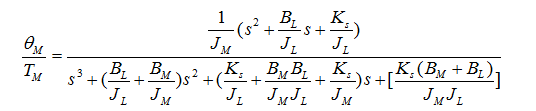   （9）

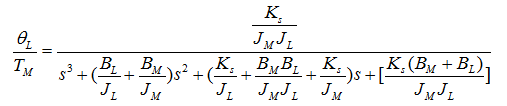  （10）

其中式（9）為電機(jī)的速度響應(yīng)、式（10）為負(fù)載的速度響應(yīng)。

θ_S是一個(gè)與表征系統(tǒng)振蕩特性的變量，忽略粘性摩擦系數(shù)，由式子（8）、（9）、（10）可得：（11）

使用一個(gè)單位階躍力矩T_S作用于系統(tǒng)，對式（11）做拉氏轉(zhuǎn)換的逆運(yùn)算可得：

     （12）

其中I_r為負(fù)載電機(jī)慣量比，即：

式（12）為表征系統(tǒng)的振蕩特性的表達(dá)式。從式（12）可以看出，增大系統(tǒng)的傳動(dòng)剛度將升高振蕩的頻率，但會(huì)降低振蕩的幅值，當(dāng)系統(tǒng)的傳動(dòng)剛度為無窮大時(shí)，振蕩消失。小范圍內(nèi)增大慣量比將小幅度的降低振蕩頻率，同時(shí)小幅度增大振蕩幅值，但是當(dāng)慣量比很大的時(shí)候，較小范圍調(diào)整慣量比的值對系統(tǒng)振蕩已經(jīng)沒有明顯的影響?？偠灾啾容^慣量比而言，系統(tǒng)的傳動(dòng)剛性是影響系統(tǒng)穩(wěn)定性的更重要的因素。

2.        慣量匹配的實(shí)用性原則

如果系統(tǒng)傳動(dòng)剛性為無窮大，那么負(fù)載電機(jī)慣量比也可以設(shè)置到無窮大。對于一個(gè)無限傳動(dòng)剛性的系統(tǒng)而言，負(fù)載慣量和電機(jī)慣量可以看做統(tǒng)一的整體，甚至可以認(rèn)為負(fù)載和電機(jī)軸是一體的，此時(shí)慣量比不再成為問題，慣量匹配原則也將失效。從上文的分析可知，負(fù)載電機(jī)慣量比并不是導(dǎo)致系統(tǒng)振蕩的主因，而只是振蕩的指示標(biāo)志，其更大的原因是系統(tǒng)的傳遞剛性，如何希望根除系統(tǒng)振蕩現(xiàn)象，更多的時(shí)候應(yīng)該從增大系統(tǒng)傳動(dòng)剛性的角度下功夫。

對于通常條件下使用到的傳動(dòng)裝置，我們也可以通過式（12）來做定性分析，從式中我們可以知道對于小范圍內(nèi)變化的負(fù)載慣量，可以通過增大系統(tǒng)傳動(dòng)剛性Ks、或是降低負(fù)載電機(jī)慣量比來規(guī)避系統(tǒng)振蕩，但是對于確定負(fù)載電機(jī)慣量比的上限，通常的辦法是利用經(jīng)驗(yàn)法則。對于常見的滾珠絲杠伺服系統(tǒng)，一般認(rèn)為當(dāng)慣量比大于10:1時(shí)系統(tǒng)對負(fù)載慣量的變化將變得十分敏感，而對于步進(jìn)電機(jī)的控制，一般認(rèn)為慣量比大于2:1~3:1時(shí)，系統(tǒng)將變得難以控制，實(shí)際上摩擦對降低振蕩是有幫助的，步進(jìn)電機(jī)的定位轉(zhuǎn)矩對吸收振蕩有一定的作用，通常情況下步進(jìn)電機(jī)的慣量比上限可達(dá)到4:1~5:1。另外對于有些伺服電機(jī)宣稱的可以達(dá)到慣量比50:1，實(shí)際上是保持系統(tǒng)穩(wěn)定性條件下明顯犧牲系統(tǒng)的加速性能的一種控制方式，并不在本文的討論范圍內(nèi)。

3.        結(jié)論

本文討論的彈性軸負(fù)載——電機(jī)傳動(dòng)模型，可以清晰直觀的幫助了解系統(tǒng)穩(wěn)定性與負(fù)載電機(jī)慣量比之間關(guān)系。但由于此模型中未提及傳動(dòng)裝置內(nèi)部摩擦、負(fù)載的反沖作用力等諸多影響伺服系統(tǒng)穩(wěn)定性的因素，在實(shí)際應(yīng)用中仍有其局限性。

參考文獻(xiàn)

[1] Jeff Moscrop, Chris Cook, and Peter Moll, “Control of Servo Systems in the Presence of Motor-Load Inertia Mismatch,” in The 27^th Annual Conference of the IEEE Industrial Electronics Socitety, Denver, USA, 2001.

[2] Richard W. Jr. Armstrong, “Load to Motor Inertia Mismatch: Unveiling The Truth,” in Drives and Controls Conference, Telford, England, 1998.